Aneb lomené výrazy a úpravy výrazů, vyloučené hodnoty s Photomathem.
Můžete si pustit následující video, nebo dočíst tento článek.
I přesto, že lomené výrazy nejsou povinně v RVP ZŠ, podívejme se společně na podmínky výrazů v aplikaci Photomath.
To, že nulou dělit nelze, můžeme žákům snadno dokázat například u zlomků. Žáci mají definovaného jmenovatele jako přirozené číslo. Tedy jmenovatel není nulový. Ostatně, jak by šel dort rozdělit na nula dílů?
S dělitelností nulou se setkáváme rovněž i u rovnic, které nemají řešení, např. 0x = 8. Nulou dělit nelze, a navíc nula krát cokoli je stále nula.
A právě to, že nulou dělit opravdu nelze, je stěžejní v rámci lomených výrazů.

Existují příklady kromě slovních úloh, které vám aplikace Photomath nevypočte, nevyřeší. Photomath vám sdělí „nezdařilo se nám rozpoznat vaši úlohu“, jak ukazuje následující obrázek. Je to proto, že aplikace neumí „přečíst“ symbol nerovná se neboli přeškrtnuté rovná se.

S tím se pojí právě podmínky řešitelnosti. Dejte žákům lomený výraz, ať určí jeho podmínky a ověří si správnost řešení s aplikací. Photomath jim poskytne odpověď, ale jinak sdělenou, než by čekali.
Objeví se „najděte vyloučené hodnoty“ – sice s postupem, ale na konci je např. a = – 3, jak ukazuje následující fotografie z aplikace Photomath. Podstatné je, aby žáci porozuměli odpovědi, kterou jim aplikace poskytuje. Aby pochopili, že aplikace hledala vyloučené hodnoty a že to jsou hodnoty právě tyto neboli tato hodnota pro neznámou „a“ se rovná -3. A aby pochopili, že my jsme chtěli podmínky, kdy se výraz nerovná nule. Tedy pokud mají v sešitě napsáno „a se nesmí rovnat -3„, mají odpověď správnou.
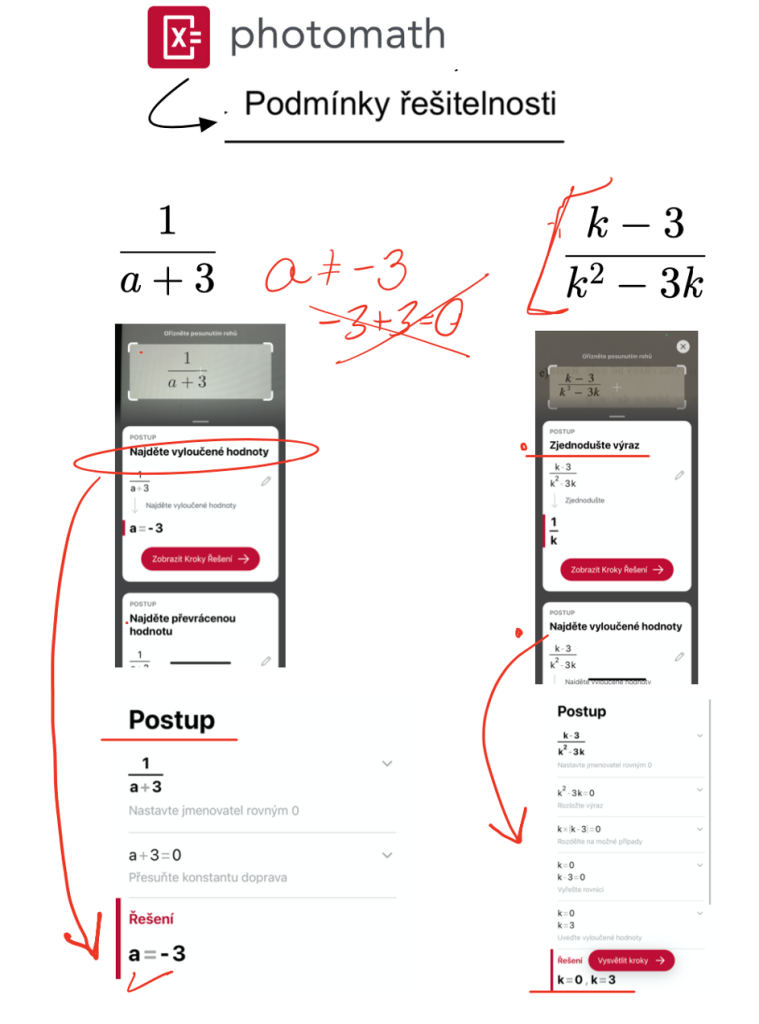
Tento rozdíl shledávám pozitivním, neboť je zde nutnost pochopení podstaty daného zadání. Je zde potřeba kritického myšlení a opětovného zkontrolování vlastního postupu. A právě kritické zhodnocení přínosu, respektive i samotného postupu a výsledku aplikací Photomath, je důležitá digitální kompetence.
(Tento konkrétní příklad obsahuje i další digitální kompetence: využití a zapojení, efektivitu a inovace a především zmíněný přínos a vývoj).
Přeji hezký den, Kateřina




