V této lekci se podíváme na to, jak můžeme využít aplikaci Photomath k vypočtení rovnice přímky.
Můžete si přečíst tento text nebo si pustit video.
Lineární funkce, konkrétně graf lineární funkce, se vyučuje v 9. ročníku. Avšak s přímou úměrností se žáci setkají již v nižším ročníku. Můžeme tak používat Photomath na grafy funkce i dříve.
Předpokladem pro použití aplikace Photomath na graf lineární funkce jsou následující znalosti žáků:
- Co je to přímka
- Pravoúhlá soustava souřadnic
- Co je a co není funkce
- Sestrojení grafu lineární funkce
- Odečítání bodů z grafu funkce
- Rovnice přímky
- Řešení soustavy rovnic
Pro názornou ukázku pro práci s žáky jsem zvolila tuto úlohu:
Napište rovnici přímky, která prochází body A[3, -2] a B[5, 2].
K vypracování použijte aplikaci Photomath.
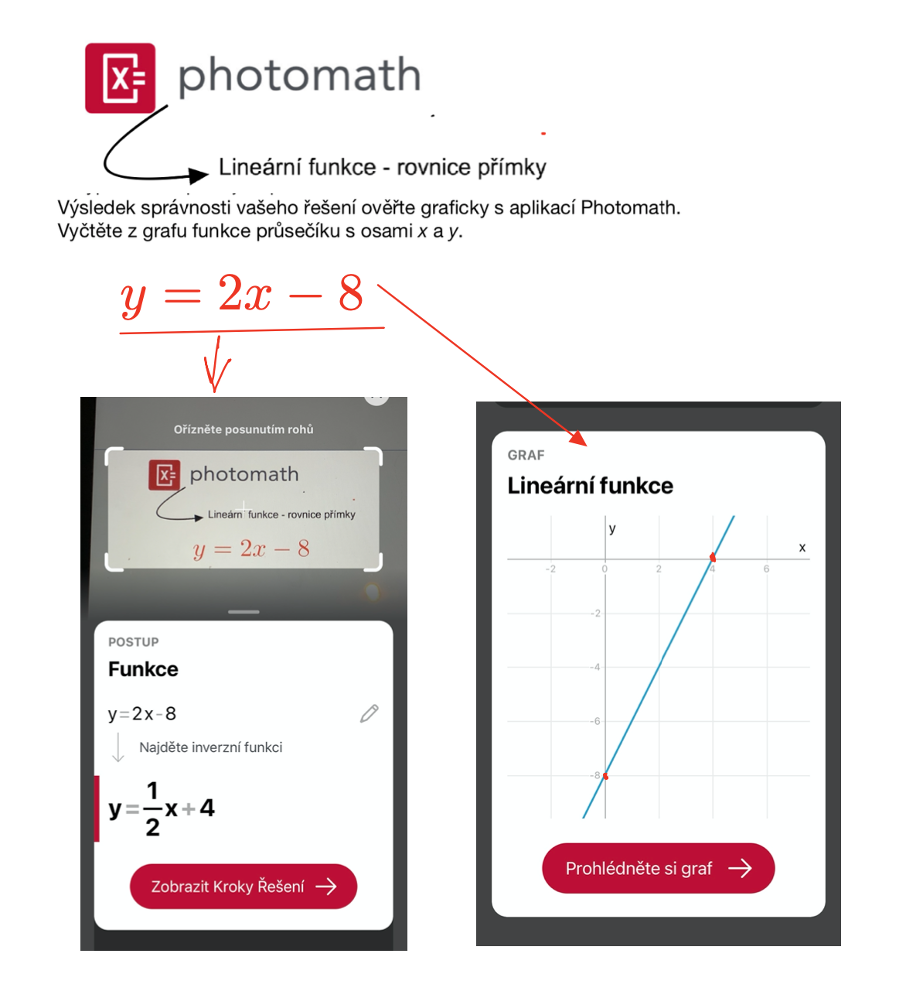
Výsledek správnosti řešení ověřte graficky s aplikací Photomath.
Z grafu funkce vyčtěte průsečíky s osami x a y.
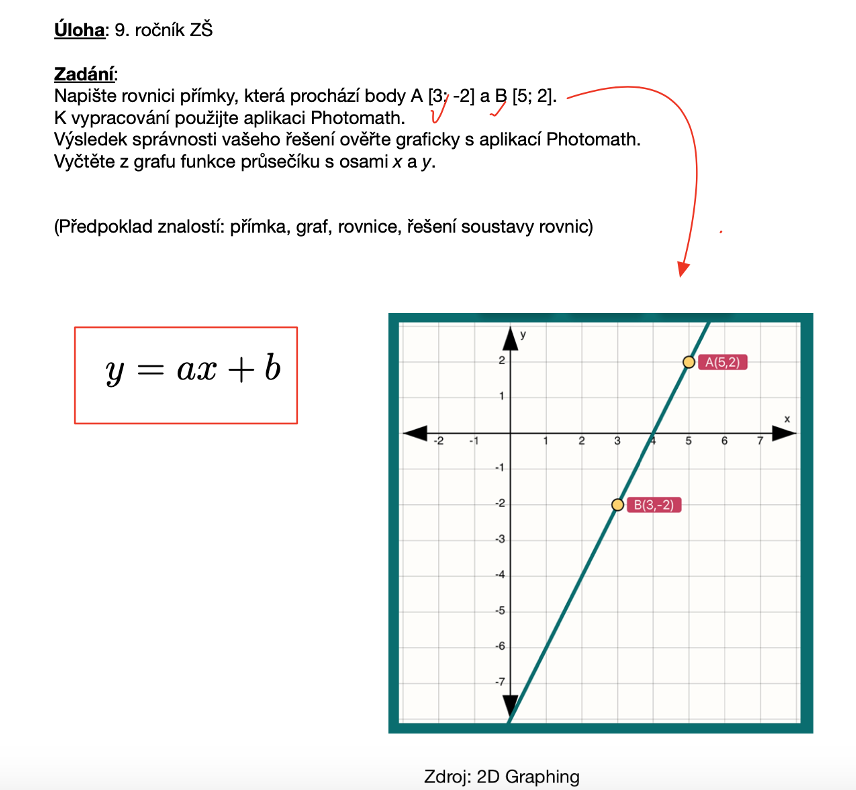
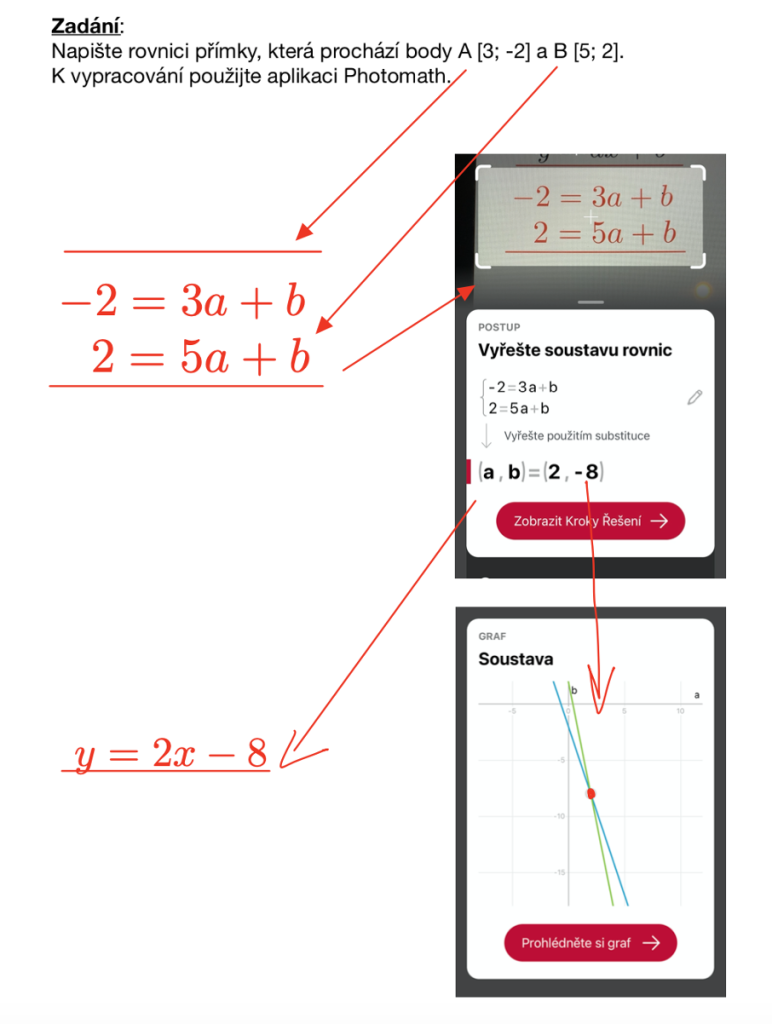
Žáci potřebují znalosti rovnice přímky, do které dosadí dva body zapsané v zadání. Poté, co žáci dosadí do rovnice oba dva body, mohou, resp. musí použít Photomath.
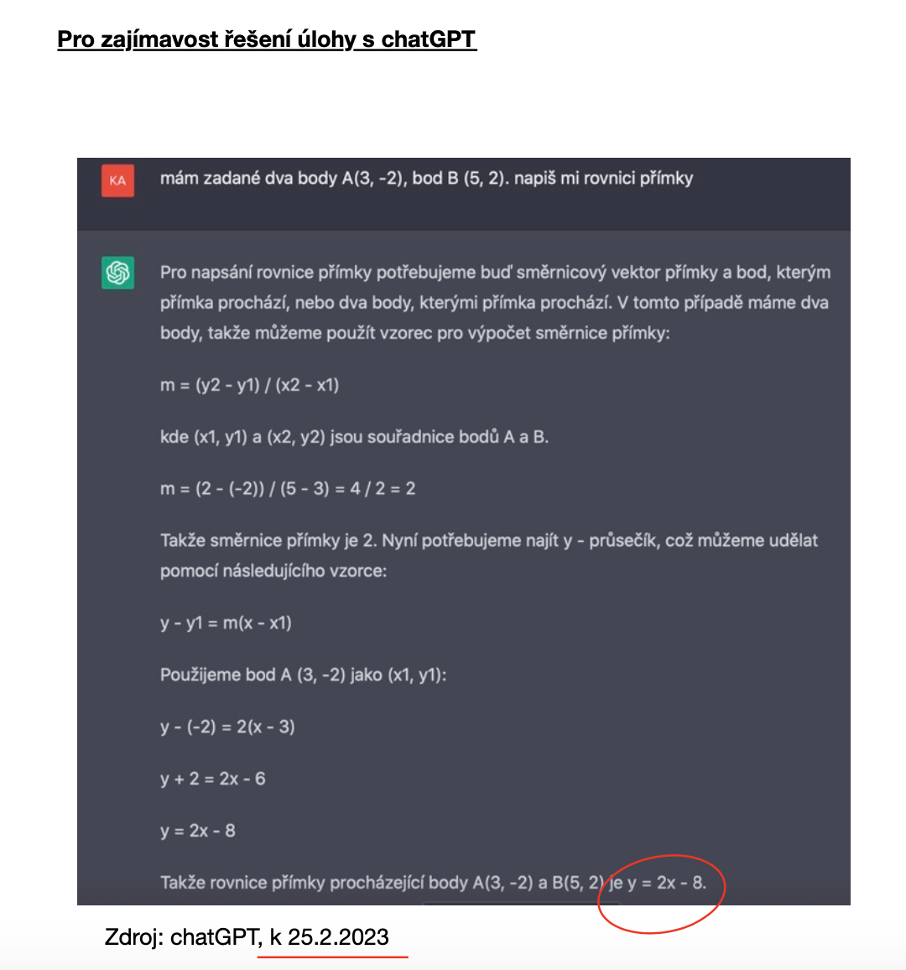
Pro zajímavost uvádím řešení i s pomocí chatuGPT. Kdo by chtěl, může žákům zpestřit hodinu i díky AI (dle podmínek společnosti OpenAI mohou ChatGPT využívat děti až od 13 let).
Při použití aplikace Photomath na lineární funkci jsou aplikovány následující digitální kompetence:
- využití a zapojení – žák používá aplikaci k řešení rovnice přímky a vytvoření grafu funkce
- efektivita a inovace – využívá digitální technologie, aby si usnadnil práci, zautomatizoval rutinní činnosti, zefektivnil či zjednodušil své pracovní postupy a zkvalitnil výsledky své práce (nové postupy, snadné vytvoření grafu funkce)
- přínos a vývoj – seznamuje se s novými technologiemi, kriticky hodnotí jejich přínosy (zhodnocení postupů, posouzení vlastní funkce – představa o funkci versus realita grafu funkce)
- informace a komunikace – komunikace ve třídě, sdílení obrázků grafů pomocí digitálních technologií
Z pohledu SAMR modelu záleží na učiteli, jak hodinu pojme.
Osobně v tomto názorném příkladu spatřuji jak vylepšení výuky, tak její proměnu.
Můžeme zadávat úkoly, které bez technologie nelze takto snadno splnit.
Největší přínos je z hlediska efektivity času a kritického myšlení, kdy žáci ověřují své výsledky řešení.
Hezký den, Kateřina




